데카르트 좌표계
하나의 점(원점) 에서 수직으로 교차하는 직선 축으로 표현되는 좌표계
2차원 : x 축 y 축으로 이루어진 2차원 좌표게
3차원 : x축 + y축 + z축
동차좌표
- n차원 투영공간을 n + 1개의 좌표로 나타내는 좌표
- 2차원 동차좌표: (Xh, Yh, h ), h != 0
2차원 데카르트 좌표와 동차좌표
- 데카르트 좌표(x,y)에 대한 동차좌표는 다음과 같이 표현한다
(hx, hy, h) , h != 0
3차원 동차좌표 표현
| 데카르트 좌표 표현 | 동차좌표표현 |
| (x, y, z) | (xh, yh, zh, h) |
| xh = hx, yh = hy, zh =hz, (h != 0) |
예
데카르트 좌표 동차 좌표
(2, 8 ,4) => 동차 파라미터가 1일때 (2, 8, 4, 1)
(1, 4, 2) => 동차파라미터가 2일때 (2, 8, 4, 2)
삼각함수
sin 함수 = 높이 / 빗변 (주기함수) sin(−𝜃) = − sin 𝜃
cos 함수 = 밑변 / 빗변 ✽ cos (−𝜃) = cos 𝜃
삼각함수의 항등식
sin^2𝜃 + cos^2𝜃 = 1
삼각함수의 덧셈정리
sin (𝐴 + 𝐵) = sin 𝐴 cos 𝐵 + cos 𝐴 sin 𝐵
cos (𝐴 + 𝐵) = cos 𝐴 cos 𝐵 − sin 𝐴 sin 𝐵
스칼라(scalar)
방향과 관계없이 크기를 나타내는 하나의 값
• 예 : 속력
벡터(vector)
방향과 크기를 함께 표현하는 기하객체
• 예 : 속도
벡터의 표현
a위치의 점을 b위치로 이동시키는 벡터 V
𝐕 = (𝑥𝑣, 𝑦𝑣)
𝑥𝑣 = 𝑥𝑏 − 𝑥𝑎
𝑦𝑣 = 𝑦𝑏 − 𝑦𝑎
예시
𝑎 = (1, 2) , 𝑏 = (7, 5)
𝐕 = (6, 3)
행렬 표현 : 열벡터 또는 행 벡터
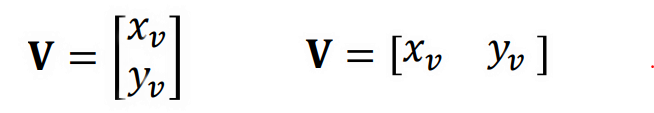
벡터의 길이
- 벡터 𝐕 = 𝑥𝑣, 𝑦𝑣 의 길이 |V|

단위벡터 : 길이가 1인 벡터
벡터 V의 정규화(동일한 방향의 단위벡터를 구하는것이다.)
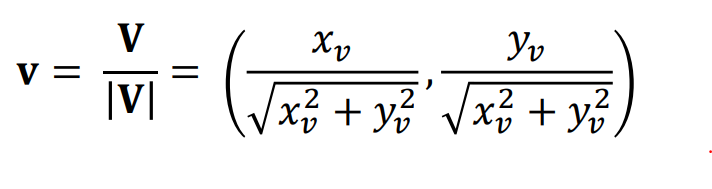
스칼라곱셈 : 벡터 𝐕와 스칼라 𝑎의 곱셈 𝑎V

벡터의 합
A = 𝑥𝐴, 𝑦𝐴 ,𝐁 = 𝑥𝐵, 𝑦𝐵
𝐀 + 𝐁 = 𝑥𝐴 + 𝑥𝐵, 𝑦𝐴 + 𝑦B
벡터 연산
내적(dot product, scalar product, inner product)
𝐀 ∙ 𝐁 = |𝐀| |𝐁| cos 𝜃 = 𝑥𝐴𝑥𝐵 + 𝑦𝐴𝑦𝐵
예)
𝐀 = 4, 1 𝐁 = 5, 3
𝐀 ∙ 𝐁 = 4 ∙ 5 + 1 ∙ 3 = 23
외적(cross product, vector product)
𝐀 × 𝐁 = 𝐀 𝐁 sin 𝜃 𝐧 = (𝑦𝐴𝑧𝐵 − 𝑧𝐴𝑦𝐵, 𝑧𝐴𝑥𝐵 − 𝑥𝐴𝑧𝐵, 𝑥𝐴𝑦𝐵 − 𝑦𝐴𝑥𝐵)
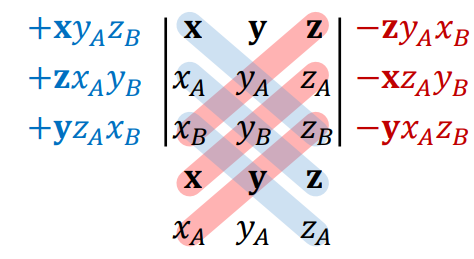
𝐱 (𝑦𝐴𝑧𝐵 − 𝑧𝐴𝑦𝐵) +𝐲 (𝑧𝐴𝑥𝐵 − 𝑥𝐴𝑧𝐵) +𝐳 (𝑥𝐴𝑦𝐵 − 𝑦𝐴𝑥𝐵)

𝐀 = (1, 0, 0) 𝐁 = (0, 1, 0)
𝐀 × 𝐁 = (0 ∙ 0 − 0 ∙ 1, 0 ∙ 0 − 1 ∙ 0, 1 ∙ 1 − 0 ∙ 0)
= (0, 0, 1)
- 이미지 출처 : 한국 방송통신대학교
'개발 > 개발지식' 카테고리의 다른 글
| [IntelliJ] 프로젝트 properties 파일 유니코드 한글 변환법 (0) | 2023.03.24 |
|---|---|
| [Javascript] 웹 화면 캡쳐하기 (Javascript, Html2Canvas) (0) | 2022.12.28 |
| [Next.js] Vercel로 배포한 환경에 .env 환경 변수 등록하기 (0) | 2022.12.22 |
| 객체 지향 프로그래밍(OOP) (0) | 2022.12.15 |
| [React] React 반응형 레이아웃 사용하기 + Typescript (0) | 2022.12.09 |


댓글